Teorema de Tales

A viagem que Tales fez ao Egito, no século VI a.C. , marcou o início da Geometria Grega e na história ficou registrado o deslumbramento do sábio de Mileto diante da Grande Pirâmide de Queops.

Construída por volta de de 2.650 a.C. e empregando cerca de 2.000.000 de blocos de pedra calcária, alguns deles com 20 toneladas de peso, aquela pirâmide eleva-se a uma altura da ordem de 146 metros.

Encontram-se frente a frente, uma das sete maravilhas do mundo antigo e um dos sete sábios da Grécia. "Que altura terá esse monumento?" perguntou-se o pai de todos os geômetras. Para responde-la, empregou um método, por ele mesmo criado e que ainda hoje nos cativa pela sua simplicidade e precisão: plantou sobre a areia, verticalmente, um bastão de madeira, cujo comprimento conhecia, e mediu-le a sombra. Após medir a sombra da pirâmide, deduziu-lhe a altura, porque sombras e alturas, tanto em piramides quanto em bastões, quaisquer que sejam seus tamanhos, são proporcionais. No momento em que a altura de um bastão é igual à sua sombra, a altura da pirâmide também será igual à sombra do monumento.

Esta proporcionalidade entre alturas e sombras constitui a essência daquilo que hoje se aprende na escola sob a denominação Teorema de Tales e, 26 séculos depois, durante a corrida espacial, os cientistas da NASA ainda avaliavam alturas de montanhas na lua e em Marte através de suas respectivas sombras obtidas em fotografias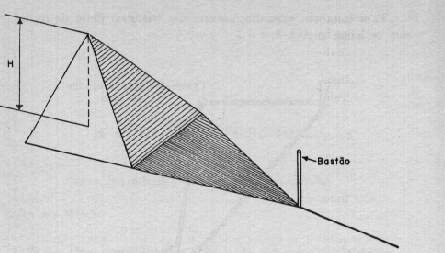




Fonte:
http://sandroatini.sites.uol.com.br/tales.htm